студент группы __-ВИЭ-__
______________
«____» ______________ 2009 г.
Работу проверил
Устич В.И.
«____» ______________ 2009 г.
Калининград
2009 г.
Задание на курсовую работу
Двухколейная железная дорога имеет между станциями А и В одноколейный участок с разъездом С. На разъезде имеется запасной путь, на котором один состав может пропустить встречный поезд. К станциям А и В поезда прибывают с двухколейных участков каждые 40 ± 10 мин. Участок пути АС поезда преодолевают за 15 ± 3 мин, а участок пути ВС — за 20 ± 3 мин. Со станции А и В поезда пропускают на одноколейный участок до разъезда только при условии, что участок свободен, а на разъезде не стоит состав. После остановки на разъезде поезда пропускаются на участок сразу после его освобождения. Поезд останавливается на разъезде, если по лежащему впереди него участку пути движется встречный поезд.
Смоделировать работу одноколейного участка железной дороги при условии, что в направлении АВ через него должны проследовать 50 составов. Определить среднее время ожидания составов на станциях А и В, а также среднее время ожидания на разъезде С и коэффициент загрузки запасного пути.
В настоящее время одним из наиболее широко распространенных средств исследования и оптимизации функционирования систем управления (и вообще любых сложных социально-технических систем) является имитационное моделирование, в основном – с применением современной вычислительной техники. ЭВМ программируется таким образом, чтобы программный продукт «жил» по законам, соответствующим условиям существования реальной системы. Далее на такой имитационной модели можно отрабатывать воздействия различных факторов, влияющих на поведение системы, изучать влияние изменения внутренних параметров на эффективность функционирования и так далее.
Процессы функционирования различных систем и сетей связи могут быть представлены той или иной совокупностью систем массового обслуживания (СМО) – стохастических, динамических, дискретно-непрерывных математических моделей. Исследование характеристик таких моделей может проводиться либо аналитическими методами, либо путем имитационного моделирования.
Выявление сущности экономики как науки и как экономической деятельности. ...
... Предоставить отчёт о выполненной работе, содержащей: порядковый номер и наименование практической работы; цель практической работы; ход выполнения работы; ответы на контрольные вопросы; вывод ... система мирового хозяйства (мировая экономика); ¦вЂ¦вЂ¦вЂ¦вЂ¦вЂ¦вЂ¦вЂ¦вЂ¦вЂ¦вЂ¦вЂ¦вЂ¦вЂ¦.. Науками, изучающими отдельные стороны экономической сферы общества, являются: история экономики; ………………………… финансы и ...
Имитационная модель отображает стохастический процесс смены дискретных состояний СМО в непрерывном времени в форме моделирующего алгоритма. При его реализации на ЭВМ производится накопление статистических данных по тем атрибутам модели, характеристики которых являются предметом исследований. По окончании моделирования накопленная статистика обрабатывается, и результаты моделирования получаются в виде выборочных распределений исследуемых величин или их выборочных моментов. Таким образом, при имитационном моделировании систем массового обслуживания речь всегда идет о статистическом имитационном моделировании.
Одним из наиболее эффективных и распространенных языков моделирования сложных дискретных систем является в настоящее время язык GPSS. Он может быть с наибольшим успехом использован для моделирования систем, формализуемых в виде систем массового обслуживания. В качестве объектов языка используются аналоги таких стандартных компонентов СМО, как заявки, обслуживающие приборы, очереди и т.п. Достаточный набор подобных компонентов позволяет конструировать сложные имитационные модели, сохраняя привычную терминологию СМО.
На персональных компьютерах (ПК) типа IBM/PC язык GPSS реализован в рамках пакета прикладных программ GPSS/PC и GPSS World. Основной модуль пакета представляет собой интегрированную среду, включающую помимо транслятора со входного языка средства ввода и редактирования текста модели, ее отладки и наблюдения за процессом моделирования, графические средства отображения атрибутов модели, а также средства накопления результатов моделирования в базе данных и их статистической обработки. Кроме основного модуля в состав пакета входит модуль создания стандартного отчета (GPSS World) GPSS/PC, а также ряд дополнительных модулей и файлов.
В данной курсовой работе, выполнено проектирование, реализация и анализ результатов выполнения поставленной задачи с помощью программы GPSS World.
В задании на моделирование объекта четко и ясно описаны система железной дороги, состоящая из одноколенного участка (состоит из двух участков AC и CB) и разъезда на участке C, и процессы, протекающие в этой системе. Поэтому нет необходимости в дополнительном изучении предметной области.
При описании системы железной дороги задано время прихода поездов к станциям A и B – 40 +/- 10 мин. Участок пути АС поезда преодолевают за 15 ± 3 мин, а участок пути ВС – за 20 ± 3 мин. Со станции А и В поезда пропускают на одноколейный участок до разъезда только при условии, что участок свободен, а на разъезде не стоит состав. После остановки на разъезде поезда пропускаются на участок сразу после его освобождения. Поезд останавливается на разъезде, если по лежащему впереди него участку пути движется встречный поезд.
Эти данные являются входными параметрами. Теперь необходимо определить, достаточно ли этих данных для создания модели и получения нужных результатов?
В задании сказано, что необходимо определить среднее время ожидания составов на станциях А и В, а также среднее время ожидания на разъезде С и коэффициент загрузки запасного пути.
Среднее время ожидания составов на станциях А и В, среднее время ожидания на разъезде С и коэффициент загрузки запасного пути – выходные переменные моделируемой системы.
Теперь проанализируем законы распределения исходных данных.
Время поступления поездов на станции A и B равномерно распределено в интервале от 30 до 50 мин, т.е. задания с одинаковой вероятностью могут поступать через интервалы 30, 31, 32, 33, 34 … 50 мин. Время преодоления участка AC равномерно распределено в интервале от 12 до 8 мин. Время преодоления участка BC равномерно распределено в интервале от 17 до 23 мин. Со станции А и В поезда пропускают на одноколейный участок до разъезда только при условии, что участок свободен, а на разъезде не стоит состав. После остановки на разъезде поезда пропускаются на участок сразу после его освобождения. Поезд останавливается на разъезде, если по лежащему впереди него участку пути движется встречный поезд.
Итак, можно сделать выводы, что исходные данные для моделирования достаточны.
Система железной дороги состоит из одноколенного участка пути AB и разъезда в точке C. На станции A и B поступают поезда. Со станции А и В поезда пропускают на одноколейный участок до разъезда только при условии, что участок свободен, а на разъезде не стоит состав. После остановки на разъезде поезда пропускаются на участок сразу после его освобождения. Поезд останавливается на разъезде, если по лежащему впереди него участку пути движется встречный поезд.
Участки пути AC и CB, а также разъезд можно представить как приборы. Тогда СМО будет выглядеть следующим образом
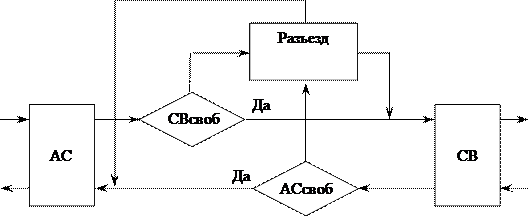 |
Рис 1 – СМО в виде блок схемы.
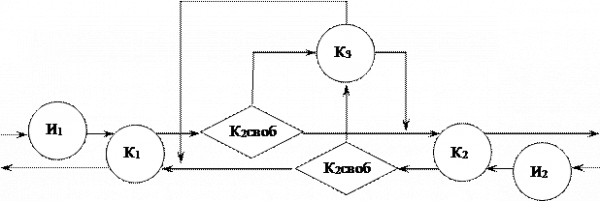
Рис 2 – СМО в виде Q – схемы.
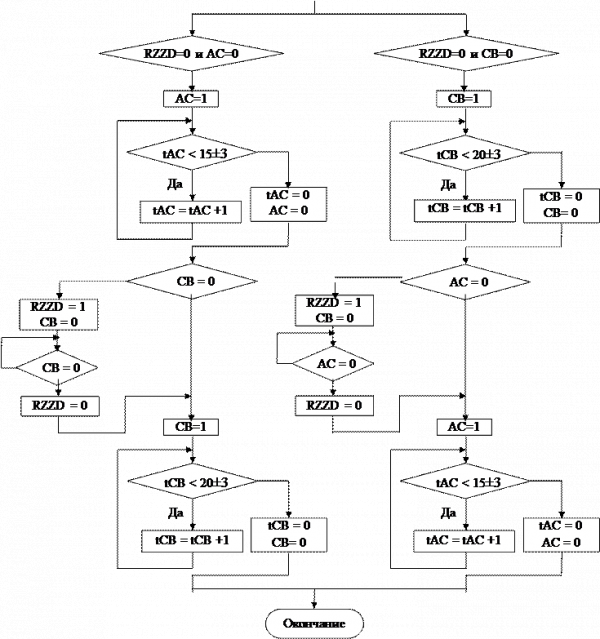
На этом этапе создается схема алгоритма, описывающая функционирование системы внутризаводского транспорта (см. рис. 3).
Она будет строиться с использованием СМО, представленной на рис 1.
Блок-диаграмма – графическое представление операций, происходящих внутри системы. Другими словами, блок-диаграмма описывает взаимодействие событий внутри системы. Линии, соединяющие блоки, указывают маршруты потоков сообщений или описывают последовательность выполняемых событий. В случае нескольких вариантов действий от блока отходят несколько линий. Если же к блоку подходят несколько линий, то это означает, что выполняемая операция является общей для двух или более последовательностей блоков. Выбор логических путей может основываться на статистических или логических условиях, действующих в момент выбора.
Блок-диаграммы получили широкое применение при описании систем. При построении блок-диаграмм, следует соблюдать определенные условия, являющиеся основой создания программы на языке моделирования. В GPSS имеется определенное количество типов блоков для задания объектов и операций над ними. Каждому блоку соответствует графическое изображение на блок-диаграмме. Стрелки между блоками указывают маршруты потоков сообщений. Далее, для того, чтобы применить язык моделирования GPSS, каждый блок блок-диаграммы заменяется соответствующим оператором GPSS.
Построение блок-диаграммы GPSS модели системы обеспечивает необходимую гибкость модели в процессе ее эксплуатации, а также дает ряд преимуществ на стадии ее машинной отладки. При построении блочной модели производится разбиение процесса функционирования системы на отдельные достаточно автономные подпроцессы. Блоки такой модели бывают основными и вспомогательными. Каждый основной блок соответствует некоторому подпроцессу моделируемой системы, а вспомогательные блоки лишь представляют составную часть машинной модели, не отражая функции моделируемой системы, они нужны лишь для машинной реализации модели, фиксации и обработки результатов моделирования.
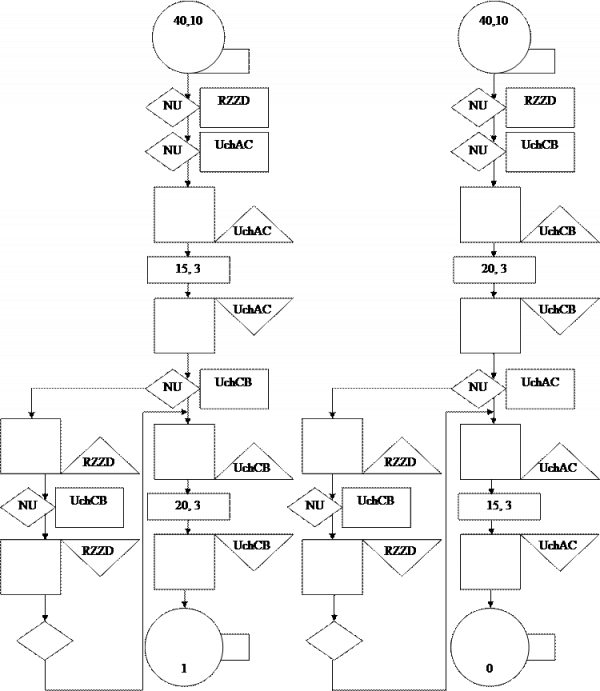
Для поставленной задачи блок-диаграмма представлена на рис. 4.
| |
||||
 |
||||
|
||||
 |
||
|
||
|
№ |
Название устройства |
Описание |
|
1 |
UchAC |
Участок AC |
|
2 |
UchCB |
Участок CB |
|
3 |
RZZD |
Разъезд |
Генерацию заявок в GPSS выполняет команда GENERATE.
Обработка в устройстве будет моделироваться блоком ADVANCE.
Выход из системы — блок TERMINATE.
Программа модели:
GENERATE 40,10
QUEUE OchUchAC
GATE NU RZZD
GATE NU UchAC
SEIZE UchAC
DEPART OchUchAC
ADVANCE 15,3
RELEASE UchAC
GATE NU UchCB,LabRZZDac
LabUchCB SEIZE UchCB
ADVANCE 20,3
RELEASE UchCB
TERMINATE 1
GENERATE 40,10
QUEUE OchUchCA
GATE NU RZZD
GATE NU UchCB
SEIZE UchCB
DEPART OchUchCA
ADVANCE 20,3
RELEASE UchCB
GATE NU UchAC,LabRZZDcb
LabUchAC SEIZE UchAC
ADVANCE 15,3
RELEASE UchAC
TERMINATE 0
LabRZZDac SEIZE RZZD
GATE NU UchCB
RELEASE RZZD
TRANSFER ,LabUchCB
LabRZZDcb SEIZE RZZD
GATE NU UchAC
RELEASE RZZD
TRANSFER ,LabUchAC
START 50
На этом этапе нужно создать план эксперимента. В задании сказано, что необходимо определить среднее время ожидания составов на станциях А и В, а также среднее время ожидания на разъезде С и коэффициент загрузки запасного пути.
Для определения среднего времени ожидания составов на станциях А и В, среднего времени ожидания на разъезде С и коэффициента загрузки запасного пути достаточно статистики, выдаваемой системой GPSS об очередях и приборах, и одного прогона модели (для определения среднего времени ожидания составов на станциях А и В воспользуемся командами QUEUE, DEPART).
На этом этапе программную модель нужно записать в файл на ГМД или ЖМД в зависимости от типа ПЭВМ с использованием текстового редактора, отладить и провести эксперименты.
После проведения эксперимента были получены листинги со статистикой об объектах моделирования.
ОТНОСИТ. ВРЕМЯ 2043.760 АБСОЛЮТ. ВРЕМЯ 2043.760
|
Время начала |
Время окончания |
Блоки |
Устройства |
Устройства хранения |
|
0.000 |
2043.760 |
34 |
3 |
0 |
|
Имя |
Значение |
|
LABRZZDAC |
27.000 |
|
LABRZZDCB |
31.000 |
|
LABUCHAC |
23.000 |
|
LABUCHCB |
10.000 |
|
OCHUCHAC |
10003.000 |
|
OCHUCHCA |
10000.000 |
|
RZZD |
10001.000 |
|
UCHAC |
10004.000 |
|
UCHCB |
10002.000 |
|
Счетчик блоков |
||||
|
Метка |
Блок |
Всего |
Текущий |
|
|
1 |
GENERATE |
51 |
0 |
|
|
2 |
QUEUE |
51 |
0 |
|
|
3 |
GATE |
51 |
0 |
|
|
4 |
GATE |
51 |
0 |
|
|
5 |
SEIZE |
51 |
0 |
|
|
6 |
DEPART |
51 |
0 |
|
|
7 |
ADVANCE |
51 |
1 |
|
|
8 |
RELEASE |
50 |
0 |
|
|
9 |
GATE |
50 |
0 |
|
|
LABUCHCB |
10 |
SEIZE |
50 |
0 |
|
11 |
ADVANCE |
50 |
0 |
|
|
12 |
RELEASE |
50 |
0 |
|
|
13 |
TERMINATE |
50 |
0 |
|
|
14 |
GENERATE |
49 |
0 |
|
|
15 |
QUEUE |
49 |
0 |
|
|
16 |
GATE |
49 |
1 |
|
|
17 |
GATE |
48 |
0 |
|
|
18 |
SEIZE |
48 |
0 |
|
|
19 |
DEPART |
48 |
0 |
|
|
20 |
ADVANCE |
48 |
0 |
|
|
21 |
RELEASE |
48 |
0 |
|
|
22 |
GATE |
48 |
0 |
|
|
LABUCHAC |
23 |
SEIZE |
48 |
0 |
|
24 |
ADVANCE |
48 |
0 |
|
|
25 |
RELEASE |
48 |
0 |
|
|
26 |
TERMINATE |
48 |
0 |
|
|
LABRZZDAC |
27 |
SEIZE |
49 |
0 |
|
28 |
GATE |
49 |
0 |
|
|
29 |
RELEASE |
49 |
0 |
|
|
30 |
TRANSFER |
49 |
0 |
|
|
LABRZZDCB |
31 |
SEIZE |
7 |
0 |
|
32 |
GATE |
7 |
0 |
|
|
33 |
RELEASE |
7 |
0 |
|
|
34 |
TRANSFER |
7 |
0 |
|
|
Устройство |
Количество обработок |
Загрузка |
Время |
Помощь |
Владелец |
Повтор |
Задержка |
|
RZZD |
56 |
0.343 |
12.524 |
1 |
0 |
0 |
0 |
|
UCHCB |
98 |
0.961 |
20.047 |
1 |
0 |
1 |
0 |
|
UCHAC |
99 |
0.710 |
14.659 |
1 |
100 |
0 |
0 |
|
Очередь |
Макс |
Текущее содержимое |
Количество обработок |
Количество обработок (0) |
Среднее содержимое |
Среднее время |
Среднее (-0) |
Повтор |
|
OCHUCHCA |
2 |
1 |
49 |
7 |
0.411 |
17.138 |
19.994 |
0 |
|
OCHUCHAC |
1 |
0 |
51 |
10 |
0.271 |
10.850 |
13.497 |
0 |
Из статистики следует, что среднее время ожидания составов на станциях А и В 10.850 и 17.138 мин. соответственно. Среднее время ожидания на разъезде С – 12.524 мин. коэффициент загрузки запасного пути – 0.343 (34,3%).
Проведем эксперимент второй эксперимент. Уменьшим время поступления поездов на станции A и B на 1 мин.
ОТНОСИТ. ВРЕМЯ 2122.749 АБСОЛЮТ. ВРЕМЯ 2122.749
|
Время начала |
Время окончания |
Блоки |
Устройства |
Устройства хранения |
|
0.000 |
2122.749 |
34 |
3 |
0 |
|
Имя |
Значение |
|
LABRZZDAC |
27.000 |
|
LABRZZDCB |
31.000 |
|
LABUCHAC |
23.000 |
|
LABUCHCB |
10.000 |
|
OCHUCHAC |
10003.000 |
|
OCHUCHCA |
10000.000 |
|
RZZD |
10001.000 |
|
UCHAC |
10004.000 |
|
UCHCB |
10002.000 |
|
Счетчик блоков |
||||
|
Метка |
Блок |
Всего |
Текущий |
|
|
1 |
GENERATE |
53 |
0 |
|
|
2 |
QUEUE |
53 |
0 |
|
|
3 |
GATE |
53 |
1 |
|
|
4 |
GATE |
52 |
0 |
|
|
5 |
SEIZE |
52 |
0 |
|
|
6 |
DEPART |
52 |
0 |
|
|
7 |
ADVANCE |
52 |
1 |
|
|
8 |
RELEASE |
51 |
0 |
|
|
9 |
GATE |
51 |
0 |
|
|
LABUCHCB |
10 |
SEIZE |
50 |
0 |
|
11 |
ADVANCE |
50 |
0 |
|
|
12 |
RELEASE |
50 |
0 |
|
|
13 |
TERMINATE |
50 |
0 |
|
|
14 |
GENERATE |
55 |
0 |
|
|
15 |
QUEUE |
55 |
0 |
|
|
16 |
GATE |
55 |
2 |
|
|
17 |
GATE |
53 |
0 |
|
|
18 |
SEIZE |
53 |
0 |
|
|
19 |
DEPART |
53 |
0 |
|
|
20 |
ADVANCE |
53 |
0 |
|
|
21 |
RELEASE |
53 |
0 |
|
|
22 |
GATE |
53 |
0 |
|
|
LABUCHAC |
23 |
SEIZE |
53 |
0 |
|
24 |
ADVANCE |
53 |
0 |
|
|
25 |
RELEASE |
53 |
0 |
|
|
26 |
TERMINATE |
53 |
0 |
|
|
LABRZZDAC |
27 |
SEIZE |
51 |
1 |
|
28 |
GATE |
50 |
0 |
|
|
29 |
RELEASE |
50 |
0 |
|
|
30 |
TRANSFER |
50 |
0 |
|
|
LABRZZDCB |
31 |
SEIZE |
8 |
0 |
|
32 |
GATE |
8 |
0 |
|
|
33 |
RELEASE |
8 |
0 |
|
|
34 |
TRANSFER |
8 |
0 |
|
|
Устройство |
Количество обработок |
Загрузка |
Время |
Помощь |
Владелец |
Повтор |
Задержка |
|
RZZD |
59 |
0.610 |
21.965 |
1 |
104 |
0 |
0 |
|
UCHCB |
103 |
0.971 |
20.013 |
1 |
0 |
3 |
0 |
|
UCHAC |
105 |
0.730 |
14.757 |
1 |
106 |
1 |
0 |
|
Очередь |
Макс |
Текущее содержимое |
Количество обработок |
Количество обработок (0) |
Среднее содержимое |
Среднее время |
Среднее (-0) |
Повтор |
|
OCHUCHCA |
3 |
2 |
55 |
5 |
0.977 |
37.718 |
41.489 |
0 |
|
OCHUCHAC |
2 |
1 |
53 |
4 |
0.592 |
23.727 |
25.663 |
0 |
Из статистики следует, что при уменьшении времени поступления поездов даже 1 мин. накапливается приличная очередь на станциях. После проведения первого эксперимента очереди на станциях A и B не создавалось. Что позволяет сделать вывод: изначальная система рассчитана оптимально нет очереди на станциях и нет резерва производительности.
В данном курсовом проекте была спроектирована СМО для поставленной задачи с использованием программы GPSS World.
Была построена концептуальная модель;
- Была проведена алгоритмизация модели и ее реализация в программе GPSS World.
Также был проведен эксперименты над представленной моделью, который показал, что изначальная система рассчитана оптимально – на станциях нет очереди и нет резерва производительности.
1. Афанасьев М. Ю. Исследование операций в экономике: модели, задачи, решения: учеб. пособие. – М.: ИНФРА-М, 2003.
2. Боев В. Моделирование систем. Инструментальные средства GPSS WORLD. – М.: БХВ, 2004.
3. Варфоломеев, В. И. Алгоритмическое моделирование элементов экономических систем: практикум: учеб. пособие / под ред. С. В. Назарова. – М.: Финансы и статистика, 2004.
4. Кудрявцев Е. GPSS World. Основы имитационного моделирования различных систем. – М.: ДМК, 2003.
5. Кудрявцев Е., Добровольский. Основы работы с универсальной системой моделирования GPSS World. – М., 2005.
6. Максимей, И. В. Имитационное моделирование на ЭВМ. – М.: Радио и связь, 1988.
7. Томашевский. Имитационное моделирование в среде GPSS. – М., 2003.
8. Тарасов В.Н., Коннов А.Л., Мельник Е.В. Компьютерное моделирование. – Оренбург, 2005.